Logistic Regression

library(tidyverse)
library(tidymodels)
library(ggridges)
library(patchwork)

Learning goals

By the end of today, you will…

use logistic regression to fit a model for a binary response variable
fit a logistic regression model in R
use a logistic regression model for classification

To illustrate logistic regression, we will build a spam filter from email data. Today’s data represent incoming emails in David Diez’s (one of the authors of OpenIntro textbooks) Gmail account for the first three months of 2012 . All personally identifiable information has been removed.

email <- read_csv("data/email.csv") |>
  mutate(spam = factor(spam))

Rows: 3890 Columns: 21
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr   (2): winner, number
dbl  (18): spam, to_multiple, from, cc, sent_email, image, attach, dollar, i...
dttm  (1): time

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

glimpse(email)

Rows: 3,890
Columns: 21
$ spam         <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ to_multiple  <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ from         <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ cc           <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 2, 1, 0, 2, 0, …
$ sent_email   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, …
$ time         <dttm> 2012-01-01 06:16:41, 2012-01-01 07:03:59, 2012-01-01 16:…
$ image        <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ attach       <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ dollar       <dbl> 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 5, 0, 0, …
$ winner       <chr> "no", "no", "no", "no", "no", "no", "no", "no", "no", "no…
$ inherit      <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ viagra       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ password     <dbl> 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ num_char     <dbl> 11.370, 10.504, 7.773, 13.256, 1.231, 1.091, 4.837, 7.421…
$ line_breaks  <dbl> 202, 202, 192, 255, 29, 25, 193, 237, 69, 68, 25, 79, 191…
$ format       <dbl> 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, …
$ re_subj      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, …
$ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ urgent_subj  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ exclaim_mess <dbl> 0, 1, 6, 48, 1, 1, 1, 18, 1, 0, 2, 1, 0, 10, 4, 10, 20, 0…
$ number       <chr> "big", "small", "small", "small", "none", "none", "big", …

The variables we’ll use in this analysis are

spam: 1 if the email is spam, 0 otherwise
exclaim_mess: The number of exclamation points in the email message

We want to use the number of exclamation points in an email to predict whether or not it is spam.

Exploratory Data Analysis

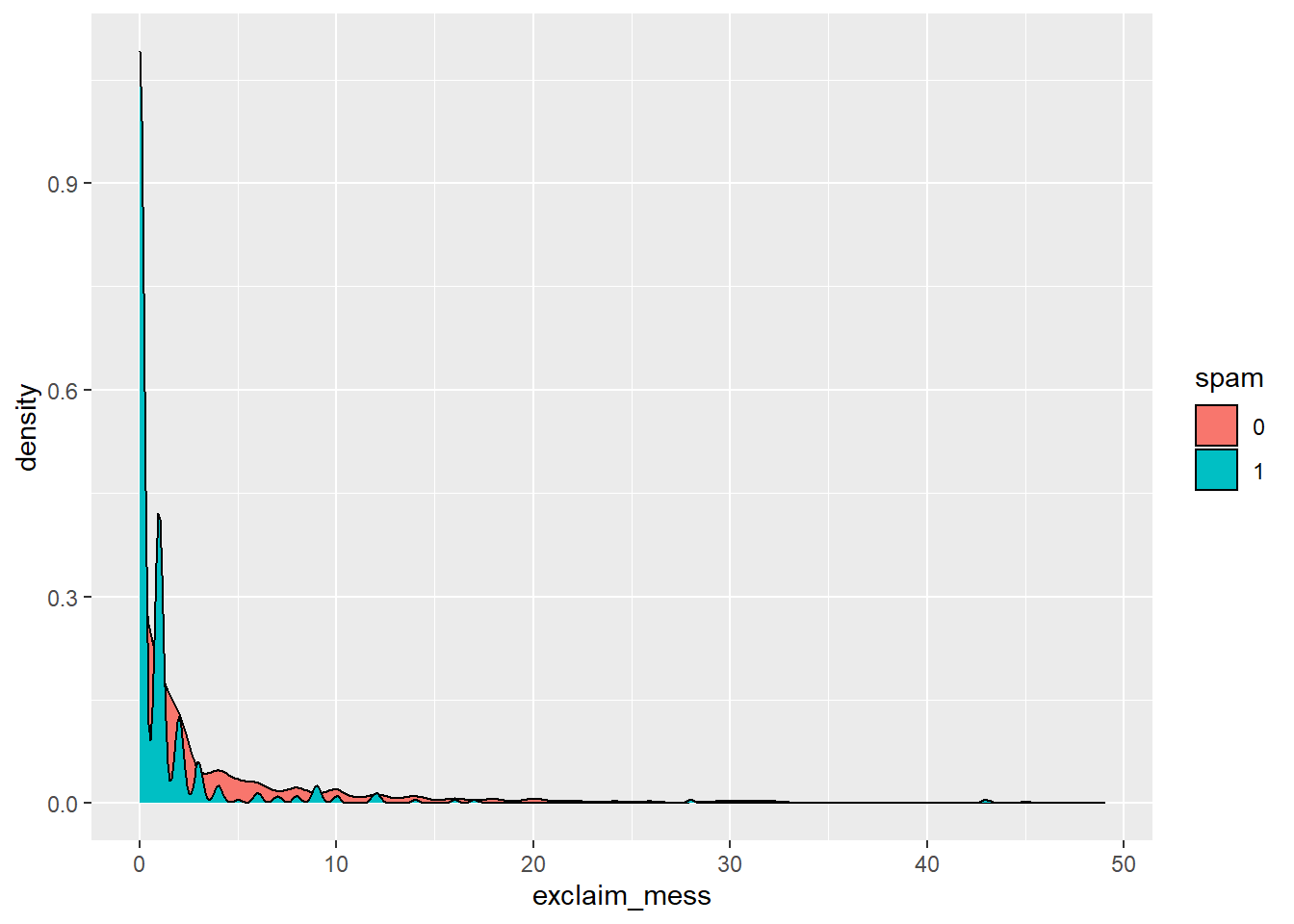
Let’s start by taking a look at our data. Create an density plot to investigate the relationship between spam and exclaim_mess. Additionally, calculate the mean number of exclamation points for both spam and non-spam emails.

email |>
  ggplot(
    aes(x = exclaim_mess, fill = spam)
  ) + 
  geom_density()

email |>
  group_by(spam) |>
  summarize(exmean = mean(exclaim_mess))

# A tibble: 2 × 2
  spam  exmean
  <fct>  <dbl>
1 0       4.04
2 1       1.27

Let’s try a linear model

Suppose we try using a linear model to describe the relationship between the number of exclamation points and whether an email is spam. Write up a linear model that models spam by exclamation marks.

spam_model_l <- linear_reg() |>
  set_engine("lm") |>
  fit(spam ~ exclaim_mess, data = email)
  
  
  
  tidy(spam_model_l)

This doesn’t work! The response variable should be numeric and not a factor if we are trying to fit a line.

A visualization of a linear model is below.

ggplot(data = email) + 
  geom_jitter(aes(x = exclaim_mess, y = spam, color = spam), alpha = 0.5) + 
  geom_smooth(aes(x = exclaim_mess, y = as.numeric(spam)), method = "lm", se = FALSE, color = "black")

`geom_smooth()` using formula 'y ~ x'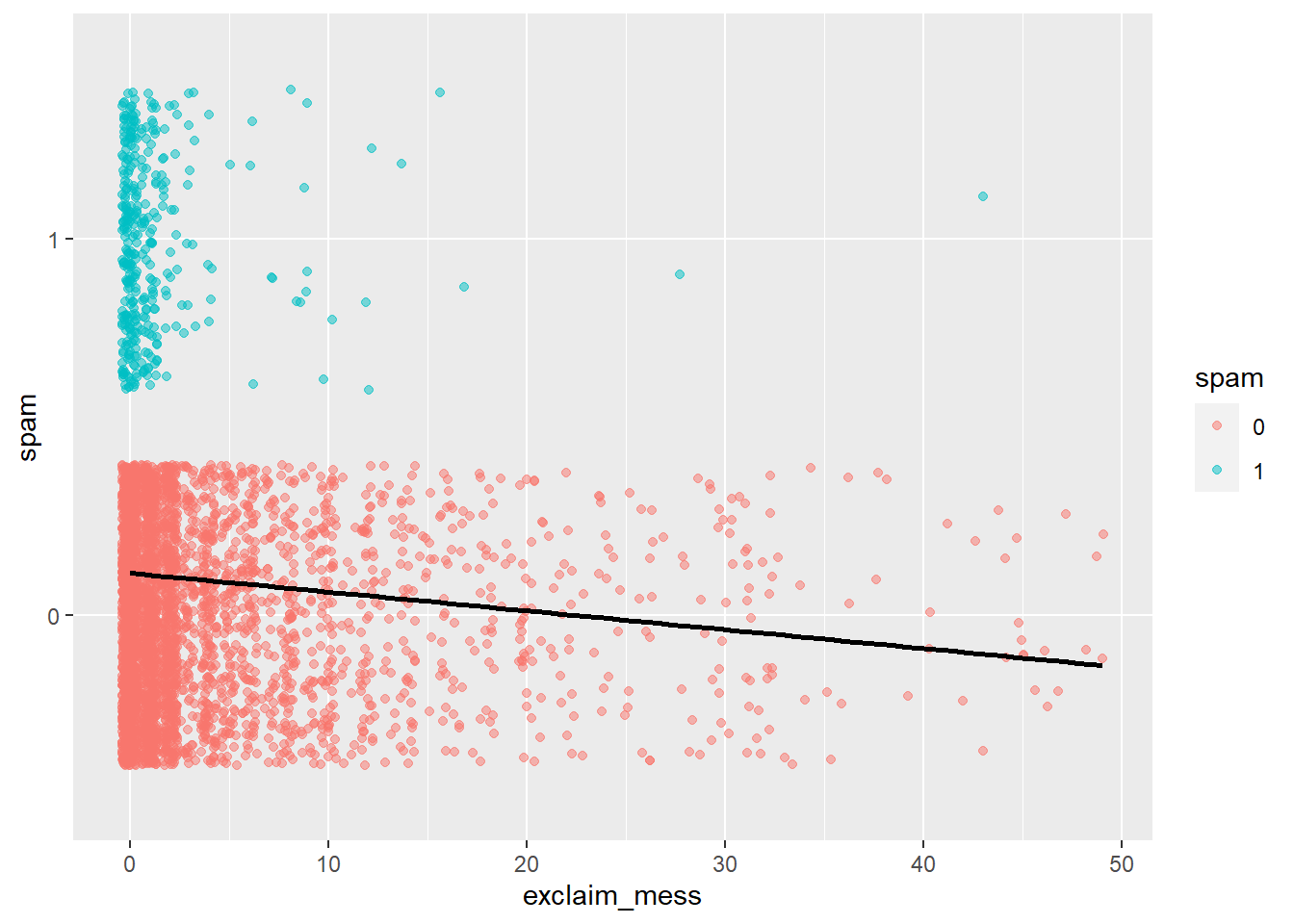

Discuss your visualization with your neighbor. Is the linear model a good fit for the data? Why or why not?

How do you build a model to fit a binary response variable (a categorical response variable with 2 outcomes)?

Logistic regression

Logistic regression takes in a number of explanatory variables and outputs the log-odds of “success” (an outcome of 1) in a binary response variable. The log-odds are then used to predict the probability of “success”.

Let’s see what the logistic regression model looks like for our example:

Let \(p\) be the probability an email is spam.

\(\frac{p}{1-p}\): odds an email is spam (if p = 0.7, then the odds are 0.7/(1 - 0.7) = 2.33)
\(\log\Big(\frac{p}{1-p}\Big)\): “log-odds”, i.e., the natural log, an email is spam

Then, the logistic regression model using the number of exclamation points as an explanatory variable is

\[\log\Big(\frac{p}{1-p}\Big) = \beta_0 + \beta_1 \times exclaim\_mess\]

The probability an email is spam is

\[p = \frac{\exp\{\beta_0 + \beta_1 \times exclaim\_mess\}}{1 + \exp\{\beta_0 + \beta_1 \times exclaim\_mess\}}\]

Exercise 1

Let’s fit the logistic regression model using the number of exclamation points to predict the probability an email is spam.

spam_model <- logistic_reg() |>
  set_engine("glm") |>
  fit(spam ~ exclaim_mess , data = email, family = "binomial")
  
  
  tidy(spam_model)

# A tibble: 2 × 5
  term         estimate std.error statistic   p.value
  <chr>           <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)    -1.91     0.0640    -29.8  9.82e-196
2 exclaim_mess   -0.168    0.0240     -7.02 2.21e- 12

How does the code above differ from previous code we’ve used to fit regression models?
Now, compare your summary output to the estimated model below.

\[\log\Big(\frac{p}{1-p}\Big) = -1.9114 - 0.1684 \times exclaim\_mess\]

Exercise 2

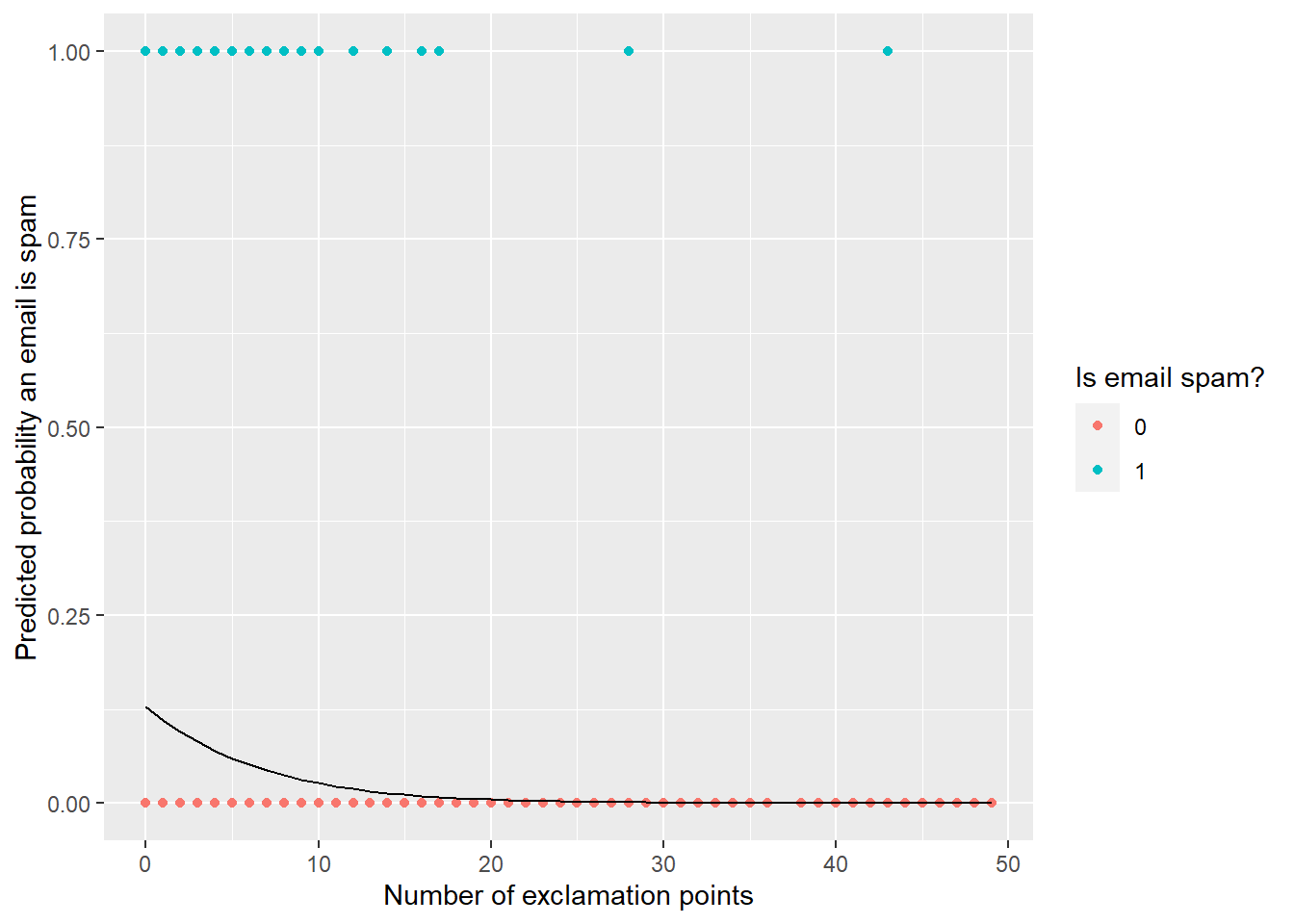
What is the probability the email is spam if it contains 10 exclamation points?

Use R as a calculator to calculate the predicted probability

-1.91 - 0.168*10

[1] -3.59

exp(-3.59) / (1+ exp(-3.59))

[1] 0.02685712

We can use the predict function in R to produce the probability as well.

new_email <- tibble(exclaim_mess = 10)
predict(spam_model$fit, new_email) # log-odds

        1 
-3.594985

predict(spam_model$fit, new_email, type = "response") # probability

         1 
0.02672713

Exercise 3

We have the probability an email is spam, but ultimately we want to use the probability to classify an email as spam or not spam. Therefore, we need to set a decision-making threshold, such that an email is classified as spam if the predicted probability is greater than the threshold and not spam otherwise.

Suppose you are a data scientist working on a spam filter. You must determine how high the predicted probability must be before you think it would be reasonable to call it spam and put it in the junk folder (which the user is unlikely to check).

What are some tradeoffs you would consider as you set the decision-making threshold? Discuss with your neighbor.

Class: I would consider the impact of recieving a spam email vs missing a potential important email.

email <- email |>
  mutate(pred_prob = predict(spam_model$fit, type = "response"))
ggplot(data = email) + 
  geom_point(aes(x = exclaim_mess, y = as.numeric(spam) -1, 
                        color = spam)) + 
  geom_line(aes(x = exclaim_mess, y = pred_prob)) + 
  labs(x = "Number of exclamation points", 
       y = "Predicted probability an email is spam", 
       color = "Is email spam?"
       )

specie <- c(rep("sorgho" , 3) , rep("poacee" , 3) , rep("banana" , 3) , rep("triticum" , 3) )
condition <- rep(c("normal" , "stress" , "Nitrogen") , 4)
value <- abs(rnorm(12 , 0 , 15))
data <- data.frame(specie,condition,value)