Models

Lecture 16

Dr. Elijah Meyer + Konnie Huang

Duke University
STA 199 - Fall 2022

October 19, 2022

Checklist

– Clone ae-14

Announcements

– Project Proposal Due Thursday

Goals

– Introduce the idea of modeling

– Why we model?

– What a model is?

– Correlation

– Introduction to probability (maybe)

Warm up

– What is the relationship?

– What is your best guess for a car’s MPG that weighs 5000 pounds?

What is a statistical model?

– Statistical modeling is the process of applying statistical analysis to a data set.

– A statistical model is a mathematical representation of observed data.

Vocab - Response variable

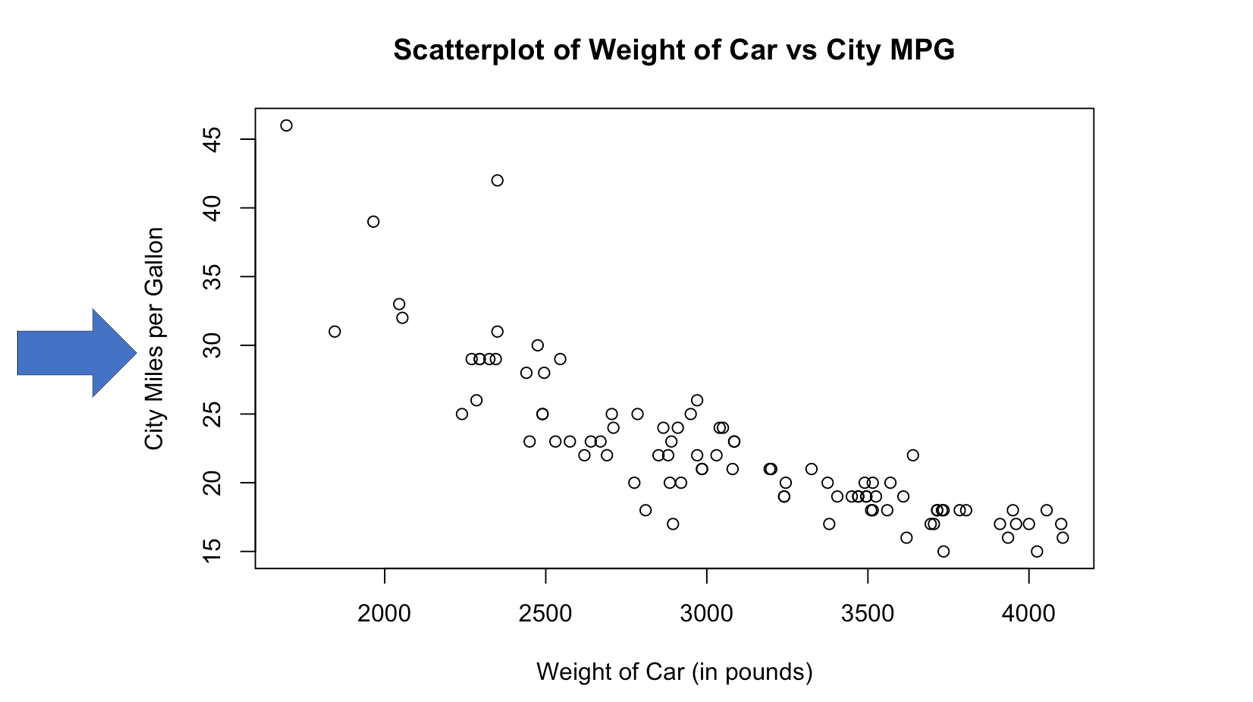
Vocab - Explanatory variable

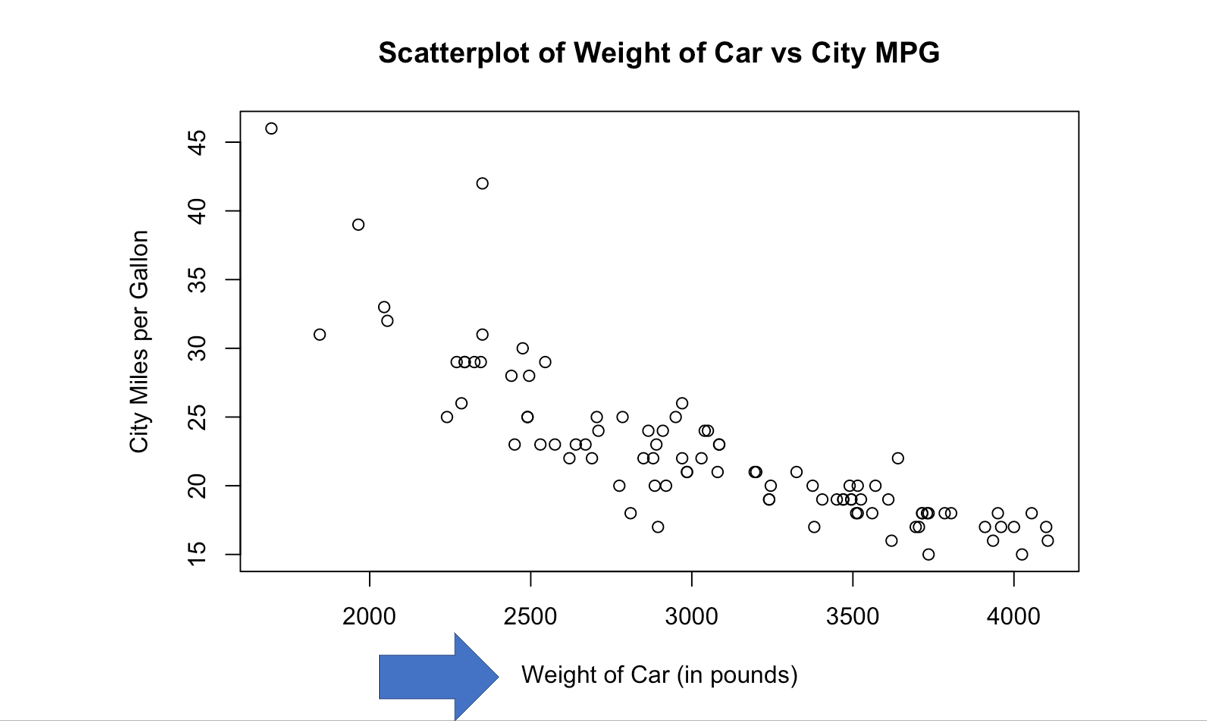
Correlation

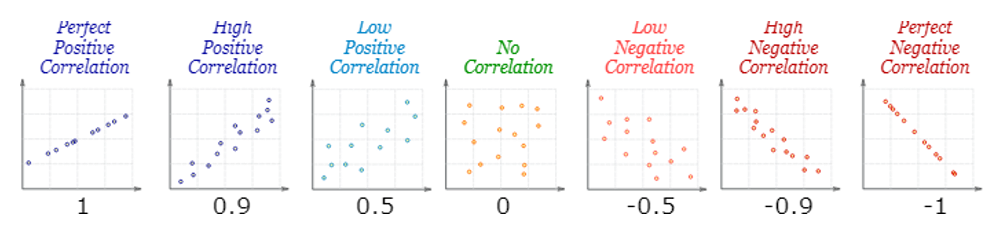
Probability

A random process is one in which the outcome is unpredictable. We encounter random processes every day: will it rain today? how many minutes will pass until receiving your next text message? will the Packers win the Super Bowl?
The probability of an event is the long-run proportion of times the event would occur if the random process were repeated indefinitely (under identical conditions).

Types of Probabilities

– Single Event

– Conditional

– And

Notation

We will denote “events” by upper case letters near the beginning of the alphabet

– P(A)

– P(A|B)

– P(A U B)

Examples

We often calculate probabilities using a table. Consider the following example:

	Cured	Not-Cured	Totals
New Drug	145	250	395
Standard Drug	300	305	605
	445	555	1,000

What is the probability of \(A\)?
What is the probability of \(B^c\)
What is the probability of \(B\) and \(A\)?
What is the probability of \(B\) given \(A\)?

Example

As a student at Duke University, suppose your first class on Mondays is in Old Chemistry at 8:00am and you commute to school. From past experience, you know that there is a 20% chance of finding an open parking spot in Lot 6. Otherwise, you have to park in Lot 18. If you find a spot in Lot 6, you only have a 5% chance of being late to class. However, if you have to park in Lot 18, you have a 15% chance of being late to class.

Step 1

“you know that there is a 20% chance of finding an open parking spot in Lot 6.”

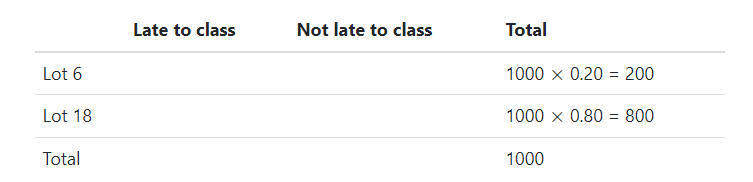
Step 2

“if you park in Lot 6, the probability of being late to class is 5%; if you park in Log 18, the probability of being late to class is 15%.

Step 3

	Late to class	Not late to class	Totals
Lot 6	10	190	200
Lot 18	120	680	800
	130	870	1,000