Hypothesis Testing

library(tidyverse)
library(tidymodels)

Learning goals

By the end of today, you will…

Use simulation-based methods to test a claim about a population parameter
Use simulation-based methods to generate the null distribution
Calculate and interpret the p-value
Use the p-value to draw conclusions in the context of the data

We have data on the price per guest (ppg) for a random sample of 50 Airbnb listings in 2020 for Asheville, NC. We are going to use these data to investigate what we would of expected to pay for an Airbnb in in Asheville, NC in June 2020. Read in the data and answer the following questions. Today, we are going to investigate if the mean price of an Airbnb in Ashville, NC in June 2020 was larger than $60.

abb <- read_csv("data/asheville.csv")

glimpse(abb)

Rows: 50
Columns: 1
$ ppg <dbl> 48.00000, 40.00000, 99.00000, 13.00000, 55.00000, 75.00000, 74.000…

Setting up the hypotheses

Based on the context of the problem, write out the correct null and alternative hypothesis. Do this in both words and in proper notation.

$\mu$ = The true / population mean price per guest for Airbnbs in in Asheville, NC in June 2020

$H_o$: $\mu$ = 60

$H_a$: $\mu$ > 60

Motivation

We want to know how unlikely it would be to observe our statistic under the assumption of the null hypothesis. Calculate and report the sample statistic below using proper notation.

#insert-code-here

abb |> 
  summarize(mean_ppg = mean(ppg)) #we use summarize when we want to calculate statistics

# A tibble: 1 × 1
  mean_ppg
     <dbl>
1     76.6

                                  #we do this by first giving it the name of the new stat and then calculating the statistic after

$\bar{x}$ = 76.6

Building a distribution

Let’s use simulation-based methods to conduct the hypothesis test specified above. We’ll start by generating the null distribution.

How do we generate the null distribution? Detail the steps below.

New idea: Shift! Shift each observation by the difference between our actual mean and our assumed population mean

Now, we resample with replacement 50 times, and take the mean of the new resampled data. <- Do this a bunch.

set.seed(101321)

null_dist <- abb |>
  specify(response = ppg) |>
  hypothesize(null = "point", mu = 60) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean") #this takes the name of the stat we are using.

Take a glimpse at null_dist. What does this represent?

glimpse(null_dist)

Rows: 1,000
Columns: 2
$ replicate <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ stat      <dbl> 54.94833, 60.20833, 48.79833, 55.28833, 64.59000, 42.30500, …

These are a bunch of resampled means under the assumption that the true mean ppg is equal to 60.

Visualize

Now, create an appropriate visualization fo your null distribution. Where is this distribution centered? Why does this make sense?

null_dist |> 
  ggplot(
    aes(x = stat)
  ) + 
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.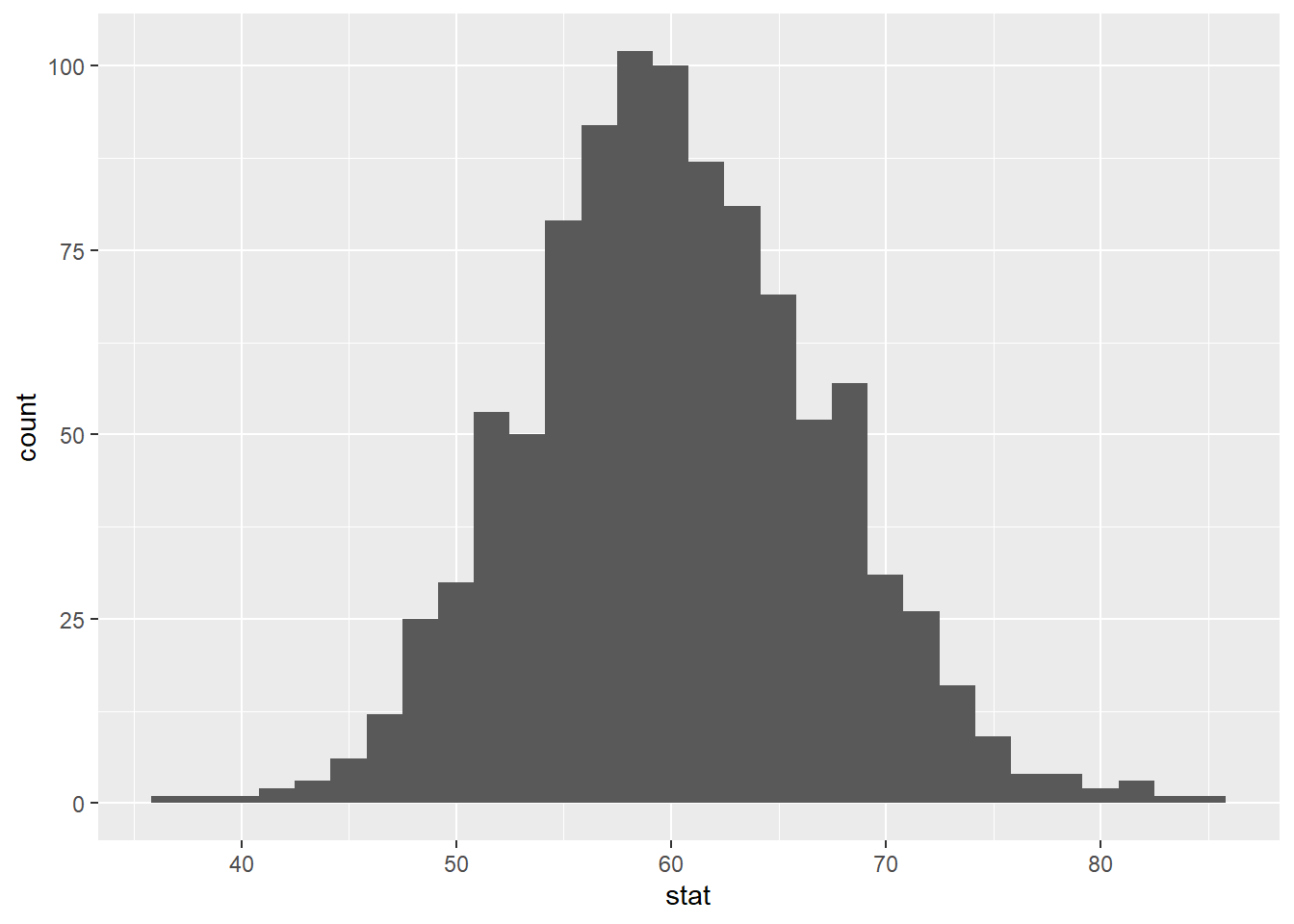

The distribution is cenetered at the null value. This makes sense because we are resampling with replacement from data who’s mean is the null value.

Now, add a vertical line on your null distribution that represents your sample statistic. Based on the position of this line, do you your sample mean is an unusual observation under the assumption of the null hypothesis?

null_dist |> 
  ggplot(
    aes(x = stat)
  ) + 
  geom_histogram() + 
  geom_vline(xintercept = 76.6)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

I would say so. Our observation is out on the tail of our distribution.

Let’s quantify your answer above….

p-value

What is a p-value?

Probability

The probability that we observe are sample statistic as extreme or more extreme given that the null hypothesis is true

How can we calculate it? Things to consider….

Add response

Let’s put this in motion!

We are going to calculate the p-value in two different ways. The first one is “by-hand”

Let’s think about what’s happening when we run get_p_value. Fill in the code below to calculate the p-value “manually” using some of the dplyr functions we’ve learned.

Calculate your p-value

null_dist |>
  filter(stat >= 76.6) |>
  summarise(p_value = n() / nrow(null_dist))

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.012

0.012

Calculate your p-value below

null_dist |>
  get_p_value(obs_stat = 76.6, direction = "greater")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.012

Let’s visualize it!

visualize(null_dist) +
 shade_p_value(obs_stat = 76.6, direction = "greater")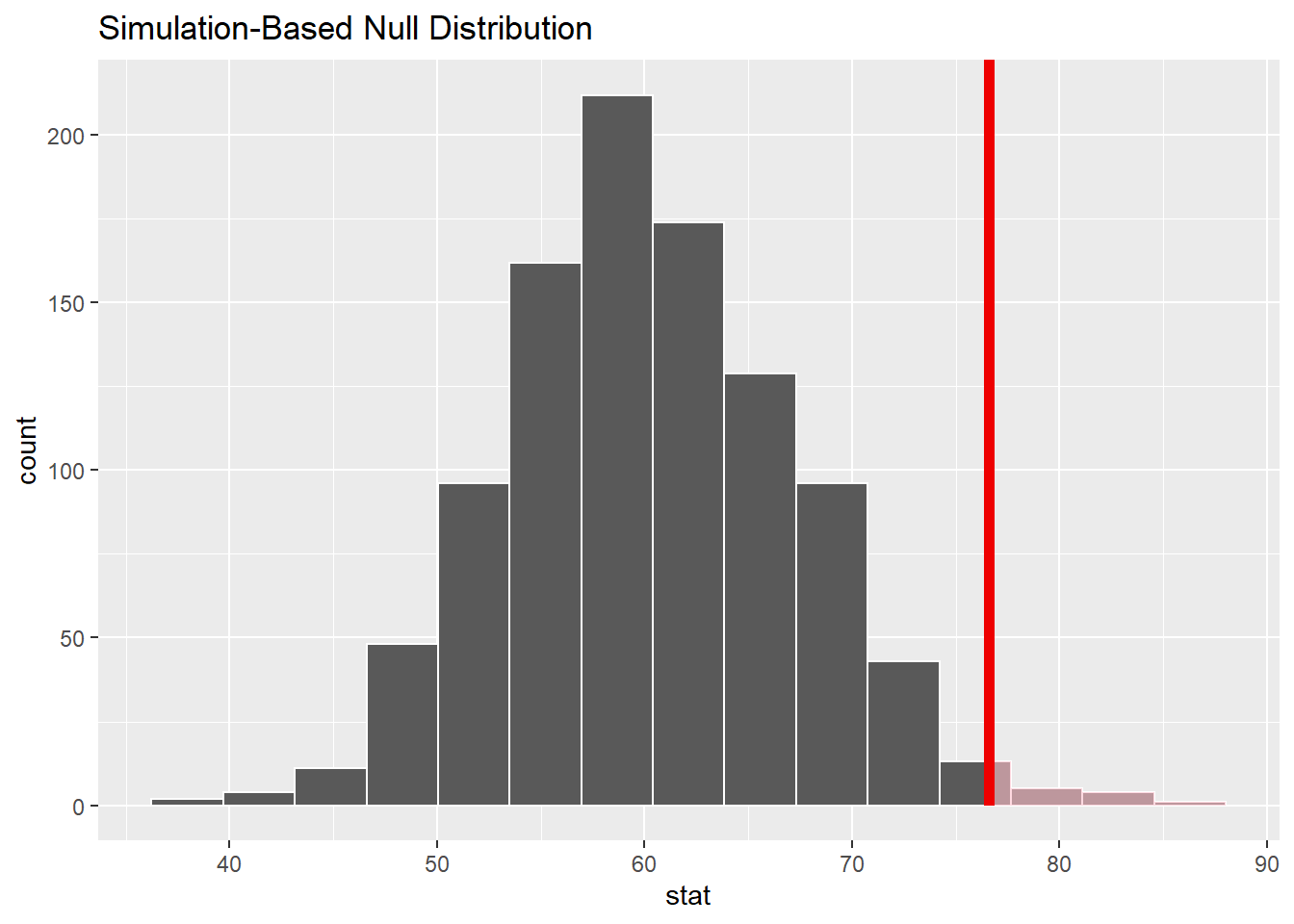

Interpret your p-value in the context of the problem

The probability that we observe are sample statistic as extreme or more extreme given that the null hypothesis is true

The probability that we observe a sample mean price of 76.6, or something greater, given that the true mean Airbnb price is equal to 60, is 0.012

Conclusion

Use the p-value to make your conclusion using a significance level of 0.05. Remember, the conclusion has 3 components

How the p-value compares to the significance level
The decision you make with respect to the hypotheses (reject $H_0$ /fail to reject $H_0$)
The conclusion in the context of the alternative hypothesis

Significance level

What is it?

$\alpha$ = a measure of the strength of the evidence that must be present in your sample before rejecting the null and concluding your alternative hypothesis

$\alpha$ = 0.05 > p-value 0.012 Reject the null hypothesis Strong evidence to conclude the alternative hypothesis

So, because our p-value is less than our significance level, we have strong evidence to reject the null hypothesis, and conclude that the true mean price per guess for airbnbs in Ashville, NC in June 2020 is larger than 60$.

Example:

$\alpha$ = 0.05 < p-value 0.120 Failing to reject our null hypothesis Weak evidence to conclude the alternative hypothesis

Two-sided

Suppose instead you wanted to test the claim that the mean price of an Airbnb is not equal to $60. Which of the following would change? Select all that apply.

Null hypothesis
Alternative hypothesis
Null distribution
p-value

Conclusion

Let’s test the claim in last exercise. Conduct the hypothesis test, then state your conclusion in the context of the data.

null_dist |>
  get_p_value(obs_stat = 76.6, direction = "two sided")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.024

Optional

We can never conclude the null hypothesis…. but why?

Let’s assume your null hypothesis for the Airbnb question is: $\mu$ = 70, and you are interested in $\mu$ > 70

null_dist2 <- abb |>
  specify(response = ppg) |>
  hypothesize(null = "point", mu = 70) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean")

visualize(null_dist2) +
 shade_p_value(obs_stat = 76.6, direction = "greater")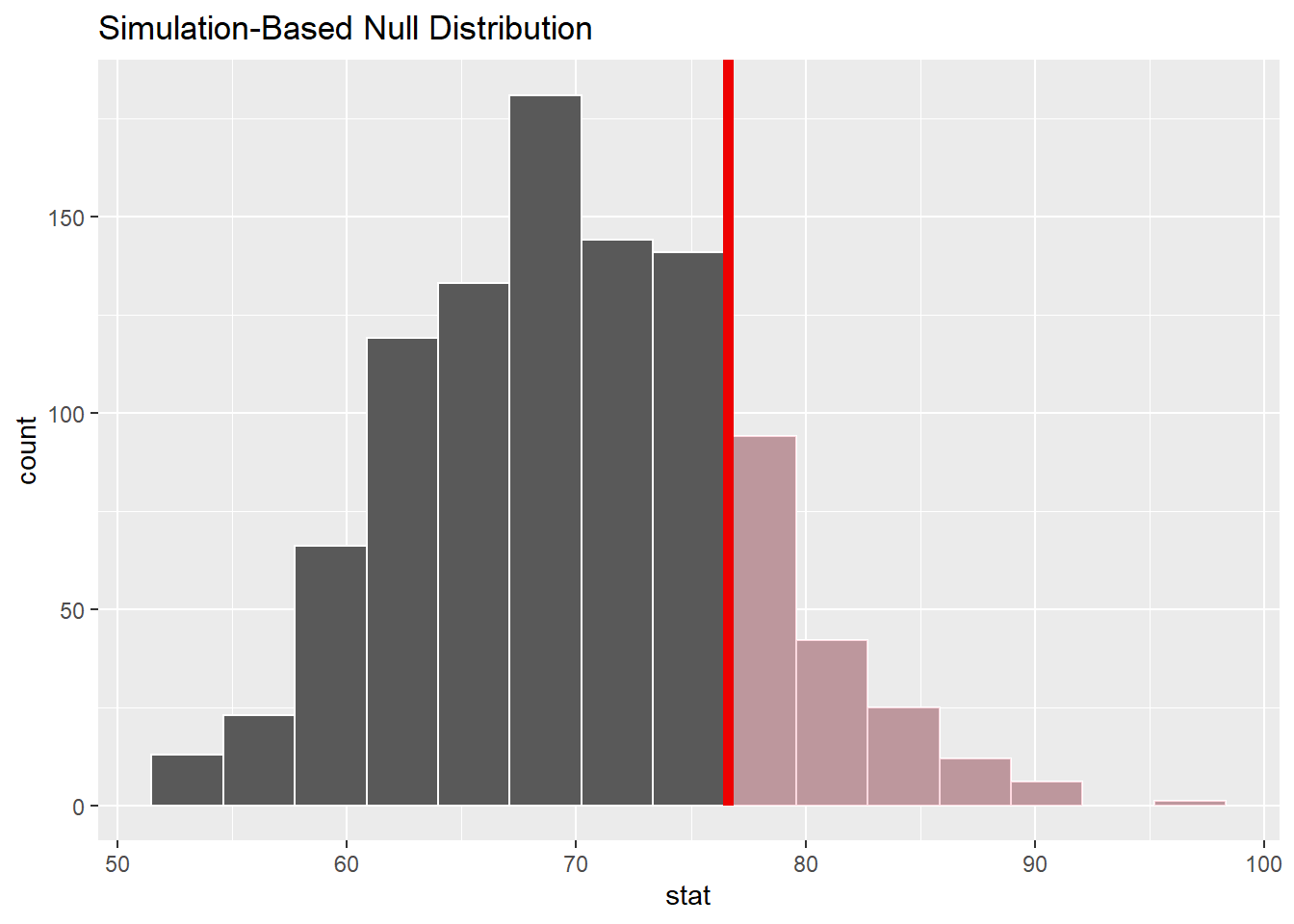

null_dist2 |>
  get_p_value(obs_stat = 76.6, direction = "greater")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.176

So now…. I incorrectly conclude that $\mu$ = 70.

Another research assumes that $\mu$ = 72….

null_dist3 <- abb |>
  specify(response = ppg) |>
  hypothesize(null = "point", mu = 72) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean")

visualize(null_dist3) +
 shade_p_value(obs_stat = 76.6, direction = "greater")

null_dist3 |>
  get_p_value(obs_stat = 76.6, direction = "greater")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.266

So now…. I incorrectly conclude that $\mu$ = 72….??????

Extra Practice

Create a new variable over50 that indicates whether or not an Airbnb price is greater than $50.

# add code

Suppose you are interested in testing whether a majority of Airbnbs in Ashville, NC in June 2020 have a price lower than $50.

State the null and alternative hypotheses.
Fill in the code to generate the null distribution.

null_dist <- ____ |>
  specify(response = ____, success = "_____") |>
  hypothesize(null = "point", p = ____) |>
  generate(reps = 1000, type = "draw") |>
  calculate(stat = "prop")

Visualize the null distribution and shade in the area used to calculate the p-value.

# add code

Calculate p-value. Then use the p-value to make your conclusion using a significance level of 0.05.

# add code