Modeling Introduction

library(tidyverse)

fish <- read_csv("data/Fish.csv")

For this activity, we will be working with a Fish data set. This data set is a record of 2 common different fish species in fish market sales. Documentation of the variables can be seen below:

variable	description
`Species`	species name of fish
`Weight`	weight of fish in grams
`Length1`	vertical length in cm
`Length2`	diagonal length in cm
`Length3`	cross length in cm
`Height`	height in cm
`Width`	diagonal width in cm

We are going to investigate the relationship between a fish’s height and weight. Below, create an appropriate plot to investigate this relationship. Add appropriate labels to the plot.

fish |> 
  ggplot(
    aes(x = Height, y = Weight)
  ) + 
  geom_point() +
  labs( 
    title = "Fish Height by Weight")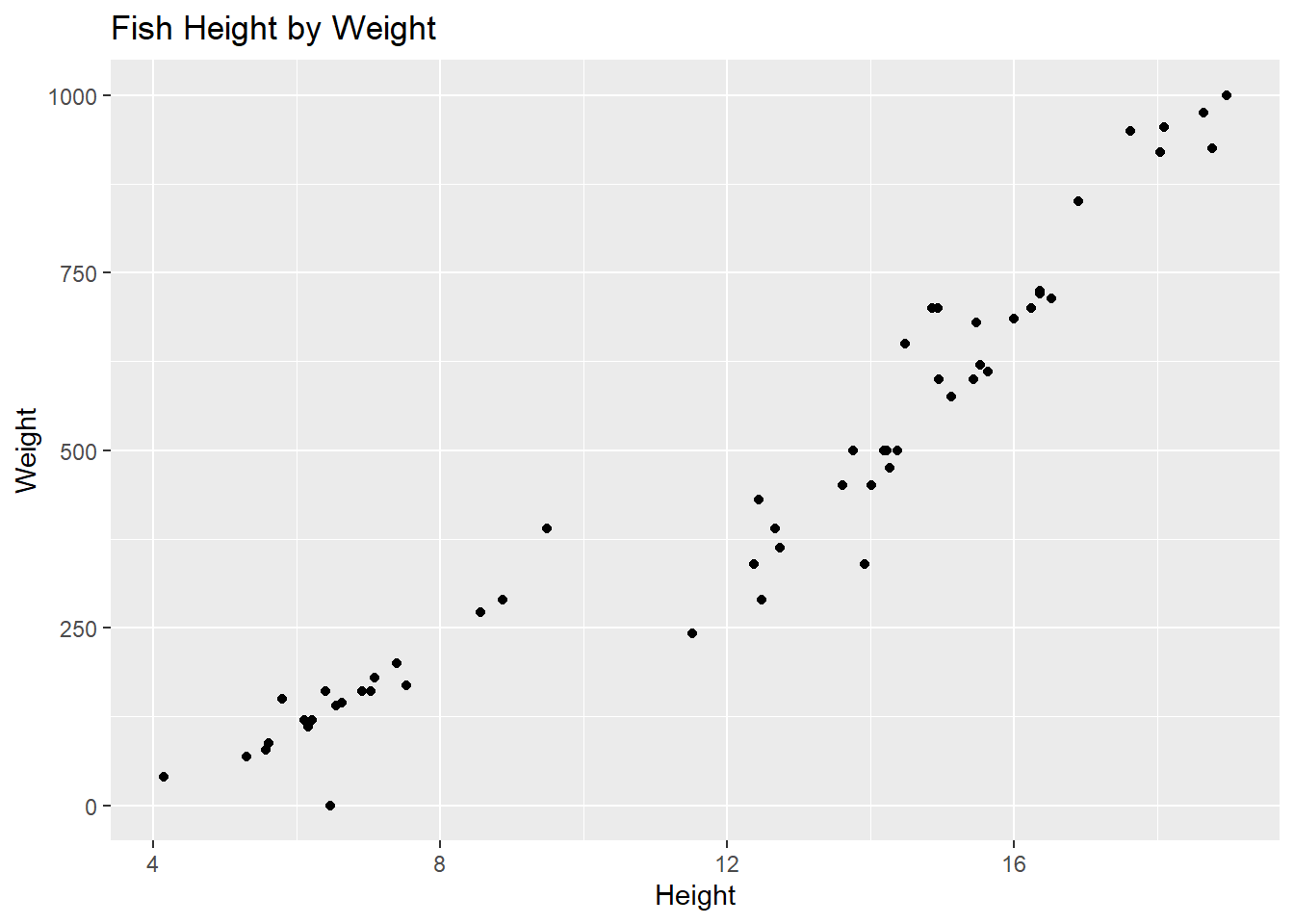

(2-min) If you were to draw a a straight line to best represent the relationship between a fish’s height and width, how would you do it?

Start from the bottom and go up Identify the first and last point and draw a line through most the others

Now, let R draw the line for us. Please refer to the documentation here: https://ggplot2.tidyverse.org/reference/geom_smooth.html. Specifically, refer to the method section.

fish |> 
  ggplot(
    aes(x = Height, y = Weight)
  ) + 
  geom_point() +
  geom_smooth(method = "lm") +
  labs( 
    title = "Fish Height by Weight")

`geom_smooth()` using formula 'y ~ x'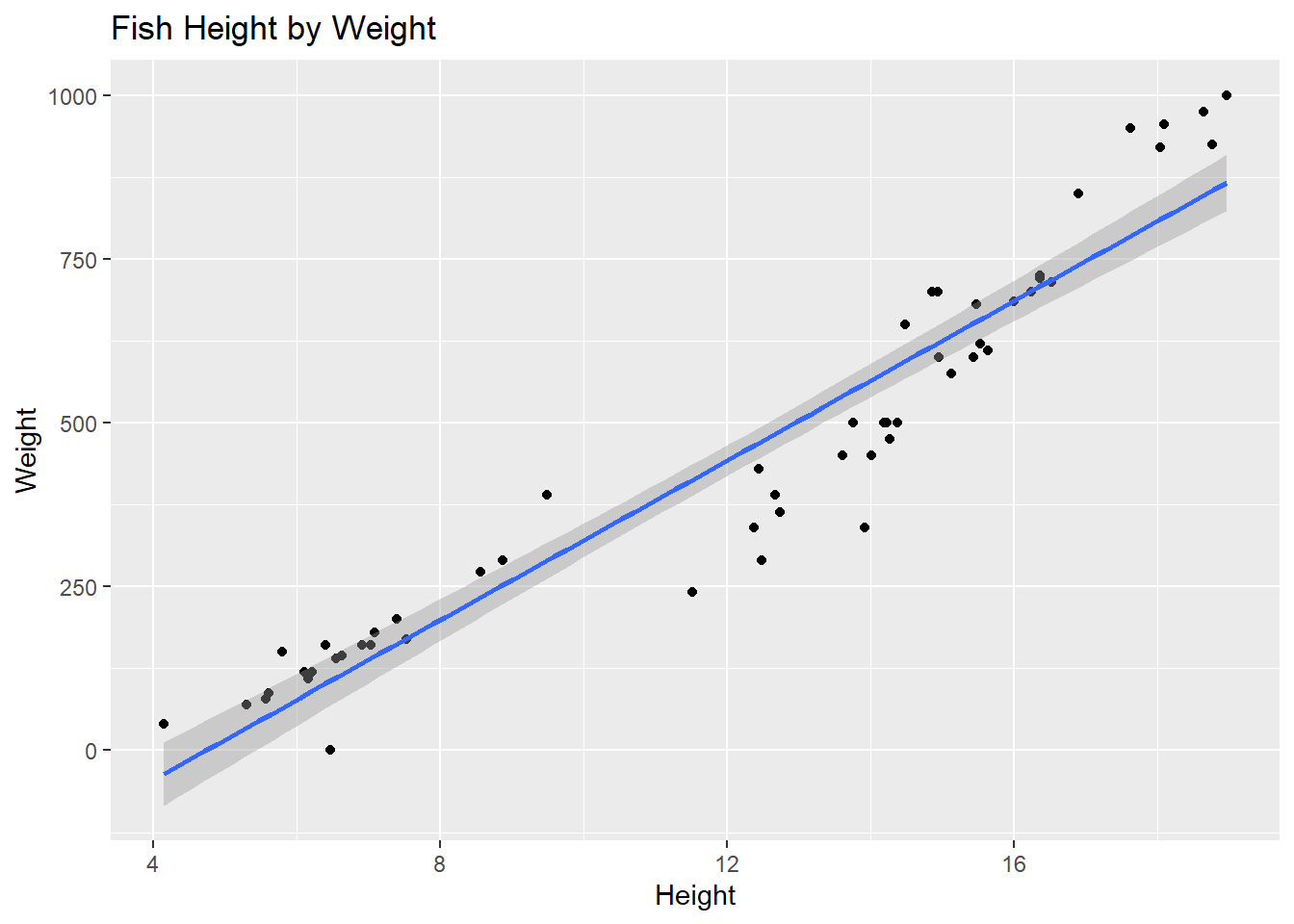

What types of questions can this plot help answer?

Is there a relationship between fish height and weight?

Predict

(2-min) We can use this line to make predictions. Predict what you think the width of a fish would be with a height of 10 cm. 15cm. 20cm. Which prediction is considered extrapolation?

At 10cm, we estimate a weight of 375 grams At 15cm, we estimate a weight of 600 grams At 20cm, we estimate a weight of 975 grams

Brainstorm. How was this line created?

R probably created a line that best fit the data….but how and what does that mean?

What is a residual?

The difference between what we observe and what our model predicts

Demo:

#Modeling Code! More on this Monday!

fit <- lm(Width ~ Height, data = fish)
fish$predicted <- predict(fit)
fish$residuals <- residuals(fit)


fish |> 
ggplot(aes(x = Height, y = Width)) + 
  geom_smooth(method = "lm", se = FALSE, color = "lightgrey") +  
  geom_segment(aes(xend = Height, yend = predicted), alpha = .2) +  
  geom_point() + 
  geom_point(aes(y = predicted), shape = 1) + 
  theme_bw()

`geom_smooth()` using formula 'y ~ x'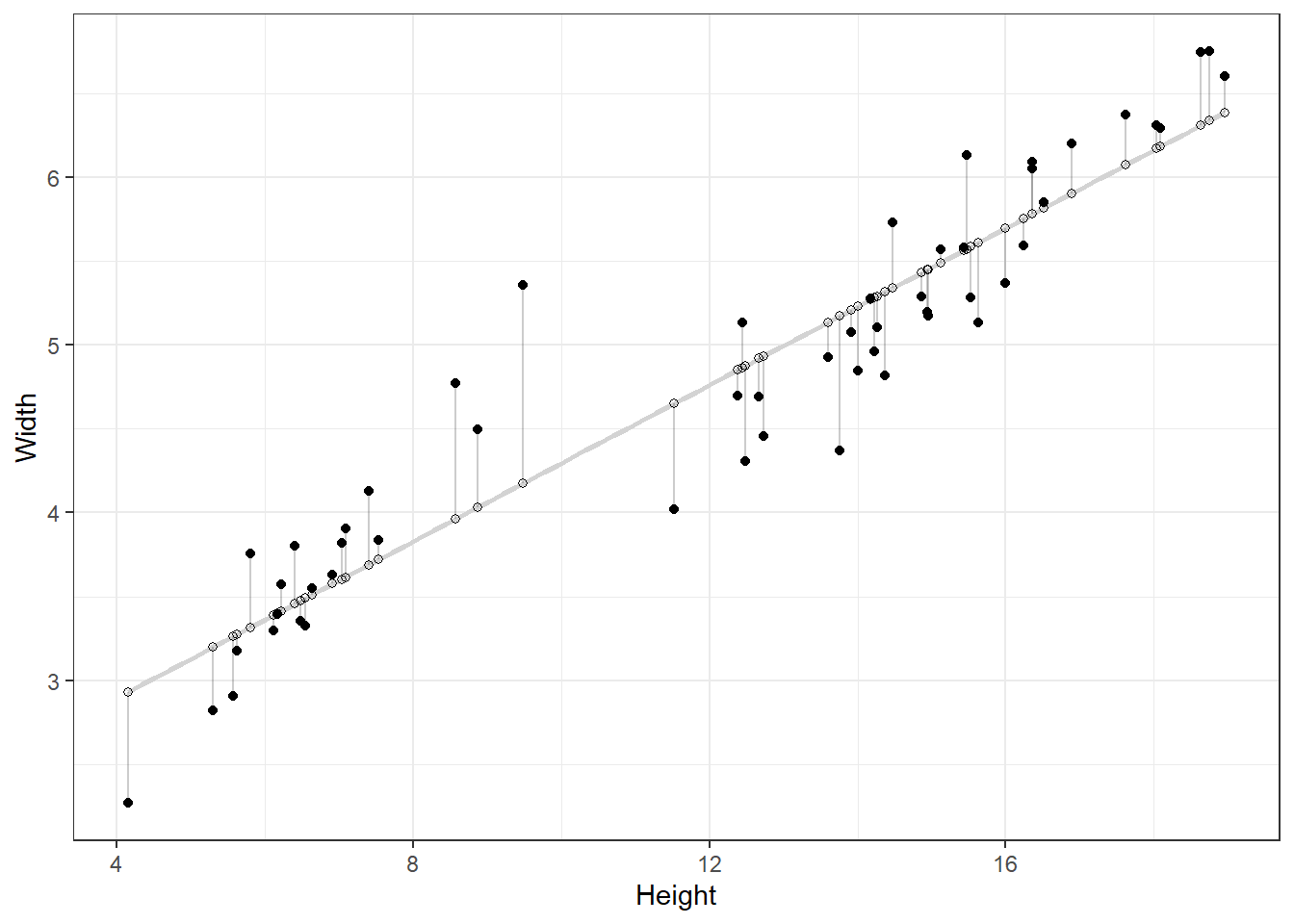

Now we know how the line is fit…. so what’s the line?

fish |>
  ggplot(
    aes(x = Height, y = Weight)
  ) + 
  geom_point() + 
  geom_smooth(method = "lm", fullrange = T) +
  labs(
    title = "Fish by Height and Width"
  ) + 
  xlim(0,20)

summary(fit)

(2-min) Using the line, predict what you think the width of a fish would be with a height of 10 cm. 15cm. 20cm.

\(\hat{weight}\) = 1.96 + 0.2310 \(\hat{weight}\) = 1.96 + 0.2315 \(\hat{weight}\) = 1.96 + 0.23*20

What is the notation of our line?

= 1.96 +0.23*height

Correlation

We can also assess correlation between two quantitative variables.

What is correlation? What is correlation bounded by?

Strength and direction of a linear relationship

r = [-1, 1]

What is the correlation between Height and Weight?

fish |>
  select(Height, Weight) |>
  cor()

          Height    Weight
Height 1.0000000 0.9537966
Weight 0.9537966 1.0000000

Are you good at guessing? Give it a try!

https://www.rossmanchance.com/applets/2021/guesscorrelation/GuessCorrelation.html

Modeling a third variable

Does the relationship change by species? Plot two separate straight lines by Bream and Roach species of fish below.

fish |> 
  ggplot(
    aes(x = Height, y = Weight, color = Species)
  ) + 
  geom_point() +
  geom_smooth(method = "lm") +
  labs( 
    title = "Fish Height by Weight")

`geom_smooth()` using formula 'y ~ x'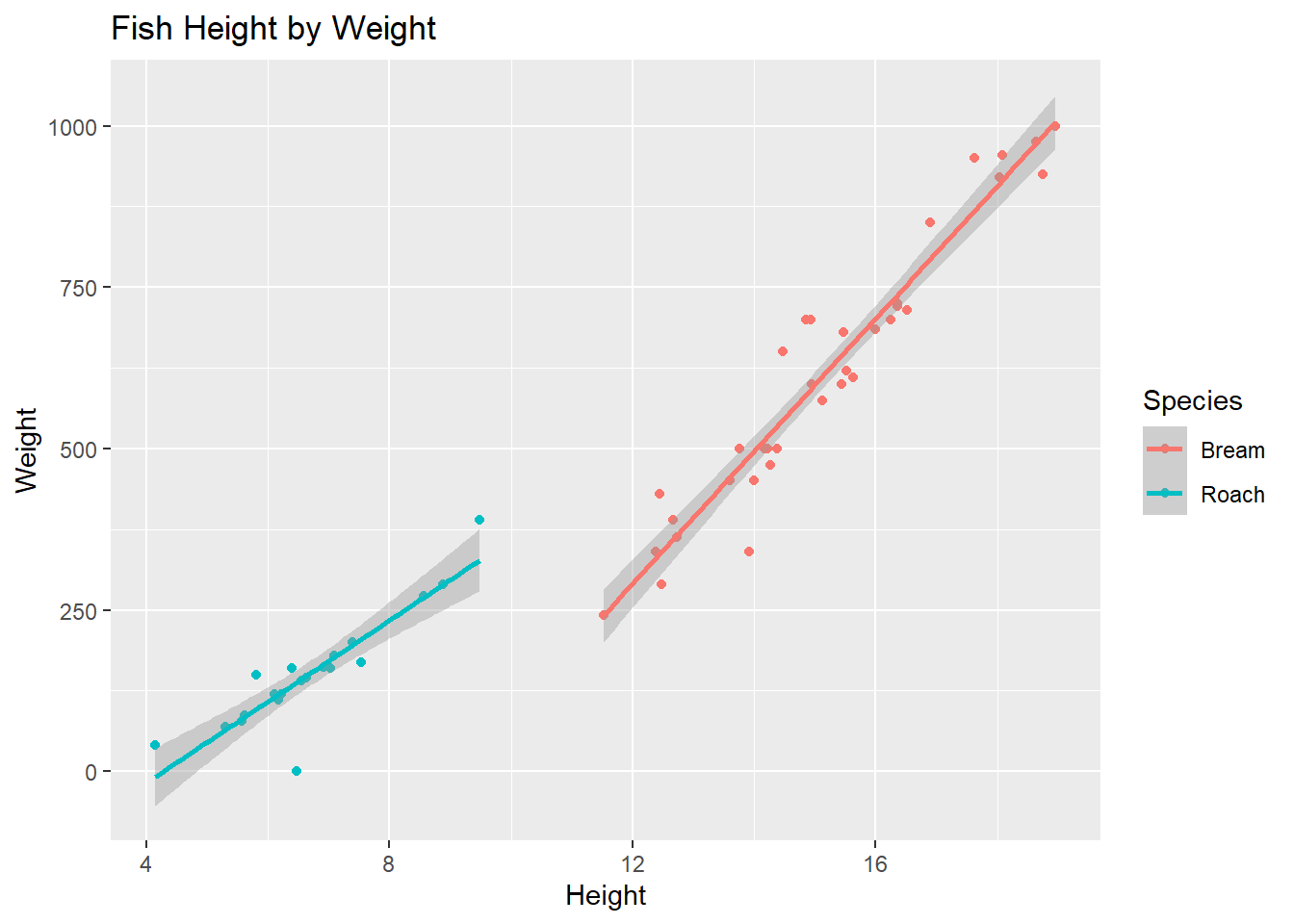

We can fit more models than just a straight line. Change the following code below to read method = loess. What is different from the plot created before?

The line isn’t straight!

fish |>
  ggplot(
    aes(x = Height, y = Width)
  ) + 
  geom_point() + 
  geom_smooth(method = "loess") +
  labs(
    title = "Fish by Height and Width"
  )